Mass/energy in the universe
The term mass/energy in the two premises reflects
the fact that all mass is comprised of energy according to Einstein's relationship
 ,
,
 .
.
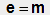
In the qm view, a body's mass m depends on the quantity and the energy of
the energy quanta in the body. And according to orthodox theory, the energy e of an energy quantum is a
function of its oscillation frequency (f) and the Planck constant (h) as follows.
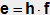
Combining the above equations we get
Due to the huge number of energy quanta moving within a body* and
the great complexity of the system of energy in a body, the energy quanta are assumed to be moving in
all directions about equally. It can be expected that the average energy of a body's energy quanta moving
parallel to a given plane will be about the same as the average energy of the body's energy quanta moving
parallel to any other plane. On the next page we model energy quanta moving in a single plane that is
representative of an entire body and we analyze how the energies of the energy quanta change when the body's
velocity through the qm changes.
 |









|
 |

