Virtual slowing of clocks and "relativistic time dilation"
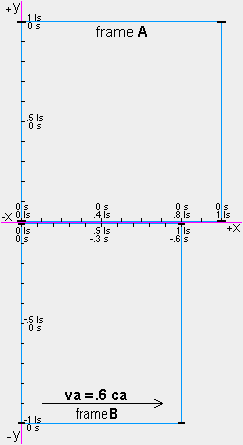
     We have shown why observers(c) aboard frame A observe a slowing of B's clocks and a foreshortening of B. These physical changes in B actually occurred. We now show why observers(c) aboard frame B observe a virtual foreshortening of A and a virtual slowing of A's clocks. The observations are the result of seeing certain clock and distance mark events that occur as frame B passes A. Each event will be specified inside brackets, [  ]. All observers on A and B see the event [The clock at the x=0 ls location on A reading 0 s is next to the clock at the x=0 ls location on B reading 0 s.] This event can be represented by [Ax=0:0 is next to Bx=0:0] where "Ax=0" and "Bx=0" specify the clocks at the x=0 ls locations on the x axes of A and B, and ":0" specifies that the time on the clocks is 0 s. The event [Ax=.8:0 is next to Bx=1.0:−.6] also occurs at ta=0 sa, as shown. The times shown on the clocks on A and B are in accordance with the Asynchronization Rule on page 12. We will use this rule and the physical change ratio equation on page 14 to determine another event that is seen by all observers on A and B.

     At time ta=0 sa, the distance between the x=.8 ls location on A and the origin on B is .8 LS and the relative velocity between the frames is .6 ca. Therefore, at time ta=1.3333 sa the event [Ax=.8:1.3333 is next to Bx=0:1.0666] occurs (as shown in figure on next page). The x=.8 ls clock on A reads 1.3333 s because rv=1 for frame A so clocks on A keep absolute time. The origin clock on B reads 1.0666 s because it was reading 0 s at time ta=0 sa and because the physical change ratio for the clock is rv=.8 so that during the 1.3333 sa it advanced only (.8·1.3333) or 1.0666 s.

     Based on these events they see, the observers aboard B conclude that the x=.8 ls clock on A moved along B from x=1 ls to x=0 ls in 1.6666 s (from −.6 s to 1.0666 s) and that during the 1.6666 s the x=.8 ls clock on A advanced 1.3333 s or only (1.3333/1.6666) or .8 times the rate of clocks on B. This virtual slowing of clocks on A as observed aboard B, and the actual slowing of clocks on B as observed on A is the so-called "relativistic slowing" or "relativistic time dilation" that relativity theory accurately predicts but attributes to relative motion between the clocks and observers. The qm view shows that the physical causes for the phenomenon involve much more than relative motion.