Modern Physics Fallacies
in the quantum medium view
Physics theory has changed greatly over the decades, and all physicists know of past theories that were eventually proven wrong.
What is not well known is what is wrong with current theory. It is important to recognize fallacies because it can help the
advancement of physics and human awareness. The qm view indicates that contemporary physics includes significant fallacies.
These fallacies are well established in people's minds and the physics literature, and they are taught to physics students and
the general public. Examples of these fallacies are contained in chapter 2 of the book, About Time,
(Simon & Schuster, 1996) by Paul Davies, a respected physicist, professor, and author of numerous books and
papers. Davies obviously has great confidence that the theory of relativity and time explained in his book is correct because
it is based on extensive experimental evidence. In the qm view, the evidence is misleading and the resulting theory is
flawed because it is based on a false assumption. Here are a few of the related fallacies.
"A theory is sound if it agrees with the related experimental evidence."
A common fallacy that appears time and again in discussions of physics theory is that a theory is sound if it agrees with
a large body of experimental evidence and can predict phenomena. Most physicists know this is a fallacy because they know of
theories that were in complete agreement with all available evidence and could predict phenomena, and were later found to be
fundamentally flawed. The qm view website cites Ptolemy's geocentric universe theory as a good example, and the Philosophy
of Science page discusses other criteria that need to be considered when assessing the soundness of physics theory. The
qm view sheds light on parts of orthodox physics theory and it shows that certain aspects of orthodox theory that Davies
and others believe are true are probably fallacies.
"A theory should not assume something exists if its existence cannot be proved by experiment."
This fallacy appears in Davies' discussion of the "ether," the light-propagating medium assumed by most physicists prior to 1900.
This fallacy should also be obvious because we now know the specifics of many things that in the past were only speculations and
could not be proved. DNA is an example of something that was once only suggested by, but not proveable by, the available evidence.
Similarly, the observed gravitational attraction between bodies indicates that something exists that is causing the gravitational
attraction (unless we want to assume that some things have no natural physical causes ‐ ‐ an assumption that is
not supported by historical evidence of humans continually finding logical physical causes for previously mysterious phenomena).
If people did not assume the existence of things like gravitons, which cannot be proved by experiment, then there would be no
theories involving these speculative things, and scientific progress would slow. The qm view shows that the apparent mutual
gravitational attraction of bodies is a logical consequence of the quantum medium, but it remains to be seen if the qm view
explanation is the best expanation. Davies writes as follows regarding the ether and the fallacy that only observable things exist.
|
There is a rule in science that says you should not introduce additional entities unless they exercise some observable
physical effect. An invisible substance that never shows up in any experiment is an entirely redundant concept.
|
Davies goes on to explain how Michelson and Morley tried to detect the ether over a century ago and could find no evidence
of the ether. The qm view shows exactly why the light-propagating medium on which the qm view is based cannot be
detected by their experiment, or by other similar experiments that were conducted over the years, but Davies is probably
unaware of this fact. The following from his book indicates that he pictures the ether being some kind of matter.
|
Now, this ether was evidently peculiar stuff, because it apparently exerted no noticeable mechanical effects -- no force or
frictional drag -- on bodies moving through it. The Earth, for example, could happily plow through the ether on its journey
around the sun without feeling the least resistance.
|
The quantum medium is not matter like the quanta of energy and matter that we can now detect and which comprise atoms,
molecules, Earth, and larger bodies. It is a medium through which energy in the form of oscillations or distortions of the
medium moves at the speed of light, which is determined by the properties of the medium. Therefore, the quantum medium must
be very unlike mediums comprised of atoms. The qm view assumes that the quanta of energy and matter that we can detect
are oscillations, or systems of oscillations, of this medium. The oscillations, somewhat like sound waves in water or glass,
move freely through the medium as the medium is distorted and recovers. They are not impeded by the medium because there is
nothing in the medium to impede them, except other oscillations. Although we can only speculate about this quantum medium and
cannot directly detect it, its existence is indicated by the wide variety of phenomena for which it provides the only common,
plausible explanation. Among these phenomena are constant light speed, c, Doppler energy shifts, inertia, the internal energy
of matter, and gravity. Possibly the quantum medium is also a physical basis for theorized "fields," "dark mass/energy," and
the "quantum foam" of quantum mechanics theory.
"The speed of light, c, is constant relative to all sources and observers of light."
The qm view shows why the observed constant speed of light, c, is a complex logical consequence of the quantum medium. It
shows that the qm view explanation for light speed, c, is far more plausible than the assumption that c is a strange fact
of nature having no cause. The qm view indicates that light speed, c, is part of a "harmony of illusions" that support one
another. Relativity theory is the result of assuming constant light speed, c. And because relativity can accurately predict
phenomena and because the theory appears to explain phenomena, it supports the constant light speed, c, fallacy. Elsewhere
on the qm view website it is shown in detail that constant light speed, c, is a remarkable illusion. It is a complex
virtual phenomenon that is supported by experimental results involving virtual observed distances and times. The following
fallacy involves virtual times and distances, and it will be explained in detail below.
"The Twins Paradox of relativity theory is not really evidence that relativity theory is flawed."
The Twins Paradox or Clock Paradox is an apparent inconsistency inherent in relativity theory. Over the years proponents of
relativity theory have tried to show that the inconsistency does not exist. Davies portrays the paradox as a bogus objection
to relativity theory by people who can't accept the fact that the theory does away with the traditional Galilean and
Newtonian concepts of universal time and distance. His book tends to perpetuate the fallacy that the paradox somehow does
not exist. You can judge for yourself after reading the qm view explanation below. The Davies' explanation involves
"a pair of twins, Ann and Betty," and it begins as follows.
|
Betty goes off in a rocket ship at close to the speed of light and returns to Earth some years later. Ann stays put. Viewed
from Earth, Betty's time is slowed, so when Betty gets back Ann should be older than Betty. But viewed from the rocket ship,
it is Earth that is moving, so Ann's time is slowed, and on return Betty should find it is she who is older. However
both accounts cannot be right: when the twins finally get together again, Betty might either be younger or older
than Ann, but not both. Hence the claim of paradox.
In fact, there is no paradox, as Einstein, who first raised the twins problem in passing in his 1905 paper, was quick to
realize. The resolution comes from the fact that the two perspectives, Ann's and Betty's, are actually not completely
symmetric. To accomplish her trip, Betty must accelerate away from Earth, cruise at uniform speed for a while, then brake,
turn around, accelerate again, cruise some more, and finally brake again to land on Earth. Ann merely remains immobile.
All Betty's maneuvers, acceleration and deceleration, break the symmetry between the two sets of observations. The principle
of relativity, remember, applies to uniform motion, not to accelerations. An acceleration is not relative; it is absolute.
Taking this into account, it is Betty who ages less. On her return, Ann would be older.
It is important to realize two things. First, the twins effect is a real effect, not just a thought experiment. Second, it
has nothing to do with the effect of motion on the aging process. You must not imagine that the years spent in the rocket
ship are somehow kinder to Betty on account of her confinement or movement through space. |
The qm view explains why Davies is wrong in telling his readers that the twins effect
"has nothing to do with the effect of motion on the aging process."
His "Ann and Betty" example itself contradicts his statement. In his example he says that Betty must "cruise at uniform
speed for a while," and we know from experiments and from relativity theory that Betty can decrease her aging relative to
Ann's aging simply by prolonging her cruising "at uniform speed" and without any change in her "maneuvers, acceleration and
deceleration." Therefore, Betty's uniform "movement through space" must be causing her to age less than Ann.
The question is, "Why?"
The qm view shows why. It shows that the aging of a twin or the rate of an atomic clock depends on its speed through
the quantum medium because the energy-exchange rate in every system of mass/energy depends on the system's speed through
the medium. (As a system's speed through the medium approaches the speed of light through the medium, the rate of energy
exchange in the system approaches zero because the average speed of the system's energy quanta relative to the system
approaches zero.) And the rate of aging of a twin or atomic clock is proportional to the rate of energy exchange in the
twin's or clock's system or reference frame. This is explained in the qm view Introduction, Part I
video and elsewhere. The quantum medium exactly accounts for the twins paradox and a variety of other phenomena for which
there are no other plausible explanations. This is strong evidence the qm view is correct.
|
Simplified clocks paradox example without accelerations
We will use a simplified version of the twins/clocks paradox (and the figures below) to compare the relativity theory
and qm view explanations of the observed phenomena. The rates of time or rates of evolution of three atomic clocks
aboard space stations R, G, and B in unaccelerated, constant-velocity motion in remote space far from any large
concentrations of mass/energy depend entirely on their motions through the quantum medium. The space stations are all moving
with different velocities relative to one another along lines parallel to a line x through space. The lines on which R, G,
and B are moving are separated just enough to avoid collisions when the space stations pass one another. The figure shows
the locations of R, G, and B (red, green, and blue rectangles) at three times, ta=0 sa, ta=5 sa, and ta=10 sa,
where ta means absolute time and sa means absolute second (as defined on the
 page).
It shows that R moves away from G and toward B, and that G moves away from R and toward B, and that B moves toward R and G.
|
 |
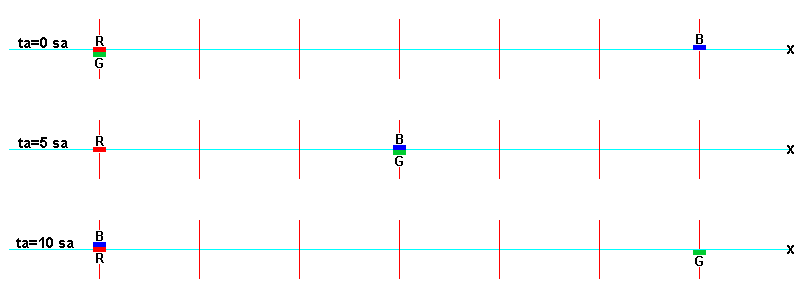When space stations R and G are momentarily next to one another at time ta=0 sa, the times displayed by atomic clocks R
and G are set to 0 s. This moment could be when a radio signal is sent between R and G or when mechanical "feelers" on the
stations make contact. Similarly, when the signal between G and B occurs at ta=5 sa, clock B is set to the time on clock G,
and when the B and R signal occurs at ta=10 sa the times on clocks B and R are recorded.
The relativity theory explanation for clock slowing due to relative motion between reference frames results in the following
paradox. Aboard space station R, relativity theory says that clocks G and B must be running slow relative to R due to their
constant-velocity motions relative to R. Therefore, the sum of the elapsed time on G as it moves from R to B and the elapsed
time on B as it moves from G to R must be less than the elapsed time on R. But aboard G, relativity says that
clock R must be running slow relative to clock G due to its motion away from G, and aboard B relativity says that R must be
running slow relative to B due to its motion toward B. Therefore, the sum of the elapsed times on G and B must be
greater than the elapsed time on R. Certainly the sum of the elapsed times on G and B cannot be both less than
and greater than the elapsed time on R, so something must be wrong with the belief that relative motion is causing the
clock slowing.
The qm view shows what is wrong with the relative motion reason for clock slowing. In the qm view, the elapsed
time on clock G as it moves from R to B plus the elapsed time on clock B as it moves from G to R will always be less than
the elapsed time on R as it moves from G to B, regardless of the observed velocities of R, G, and B relative to one another
and regardless of their velocities through the quantum medium. We will give an example to provide some understanding of
this view and the paradox. The example will not be easy to understand for someone unfamiliar with the qm view, but it
will help understand this view. A glossary of terms and symbols is available by clicking this
icon,
and it will help make sense of the explanation. Also, if you read and understand the
 page,
the example will be much easier to understand.
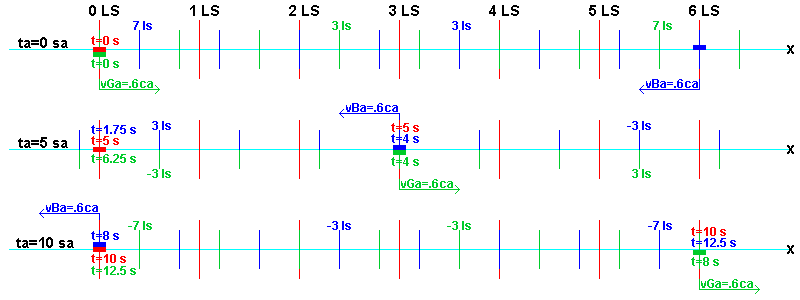
To simplify the example we will let R be at rest in the quantum medium, and let the distance between R and B be 6 LS
at time ta=0 sa, as shown. The red distance marks are 1 LS apart. We will let the absolute velocities of G and B
(i.e. vGa and vBa) be .6 ca, as shown. These velocities results in a physical change ratio of
rvG = rvB = (1−.6 ) =
.8 for these clocks. Because R is at rest in the qm, vRa=0 ca and rvR =
(1−0)= 1.
Therefore, the distances observed in reference frame R are absolute distances and the seconds specified by clock R are
absolute seconds. Clocks G and B meet at time ta=5 sa because they were 6 LS apart at ta=0 and have a closing speed
of 1.2 ca. The elapsed time on clock G at ta=5 sa is (5 sa · rvG) or 4 s.
And another 5 sa is required for B to travel to R, during which time clock B advances
(5 sa · rvB) or 4 s and clock R advances another 5 s because rvR=1. Therefore the total
elapsed time on clock R is 10 s and the sum of the elapsed times on G and B is 8 s, as shown at lower-left
in the figure. This is the relativity-theory-predicted time slowing for clocks G and B observed in frame R.
|
 |
Virtual distances and times in reference frames G and B
To show why the observations in G and B make sense to the observers, we need to determine their observations.
Their observations are based on radar measurements, the times on clocks R, G, and B that are continuously broadcast by
space stations R, G, and B respectively, and the assumption that the speed of the radar/radio signals is c relative to
every observer. Consequently, all observers know that R and G were next to one another when clocks R and G were set to
0 s, and that G and B were next to one another when clocks G and B were reading 4 s, and that B and R were next
to one another when B was reading 8 s and R was reading 10 s.
Distances in frames G and B
The figure shows the distance scales of reference frames G and B with green and blue lines every virtual
light-second, ls, from the space stations. It will help understand this example to imagine
that space stations R, G, and B have rigid rulers attached to them and that the red, green, and blue distance scales are
painted on rulers R, G, and B respectively. Imagine also that the time at any location along a ruler is specified by a clock
attached at that location which an observer with the clock has synchronized with the space station clock. Also, do not confuse
the labeled distances in ls with the times in s. The distance scales show that in reference frames G and B the
6 LS distance between G and B at time ta=0 sa is 7.5 ls. For example, a radar signal from G, traveling through
the qm with velocity 1 ca in the direction of G's .6 ca absolute velocity through the qm, is moving with a velocity
of only .4 ca relative to frame G, and it takes (6 LS / .4 ca) = 15 sa to travel
6 LS along ruler G. The return signal, traveling with a velocity of 1.6 ca relative to ruler G, takes
(6 LS / 1.6 ca) = 3.75 sa to reach space station G. Therefore, the round-trip time for the
radar signal is 18.75 sa, which is (18.75 sa · rvG) = 15 s on clock G, which is
twice the distance to the 7.5 ls virtual distance mark in frame G.
Times in frames G and B
Due to the observers' assumption of constant light speed, c, the time in reference frames G and B depends on the location
in the reference frames. For example, at ta=5 sa the time aboard space station G is 4 s (as shown in green), but
the time 3.75 ls away, where R is momentarily located in frame G, is 6.25 s because at space station G the
observers know that the time broadcast by a clock 3.75 ls away takes 3.75 s to reach them and that they should
therefore observe the 3.75 ls clock reading .25 s when their clock is reading 4 s.
But the time information broadcast by a clock 3.75 ls or 3 LS away where R is located has a velocity of only
.4 ca relative to G and it takes (3 LS / .4 ca) = 7.5 sa to reach station G. Therefore,
at ta=5 sa, the time in frame G where R is located must be (7.5 sa · rvG) = 6 s
in frame G later than .25 s, which is 6.25 s, as shown in the figure (not 3.75 s later than .25 s,
as assumed aboard G).
At ta=5 sa, an observer with a clock at the 3.75 ls location in frame G will receive the space station time
that was broadcast (3 LS / 1.6 ca) = 1.875 sa earlier or (1.875 sa · rvG)
= 1.5 s earlier on clock G or (4 s − 1.5 s) = 2.5 s on clock G.
And the observer believes that the 2.5 s broadcast time took 3.75 s to reach her, and that her clock reading
(2.5 s + 3.75 s) = 6.25 s is synchronized with space station clock G.
Page 12 of the qm view website also explains the causes of the absolute asynchronizations of clocks in
reference frames moving through the qm, and it provides a "Rule" for determining the amount of time asynchronization between
any two locations in a reference frame. The times shown in the figure are the times that result in the virtual
synchronization of clocks in frames R, G, and B. (In frame R the clocks are absolutely synchronized as well as
virtually synchronized because the speed of light in frame R is actually isotropic, as the observers assume.)
Why the distances and times observed in reference frames R agree with relativity theory.
All the observers are aware of the times on clocks R, G, and B as they pass one another, and it makes sense to observers
aboard station R that clock B is reading 8 sa when it passes clock R reading 10 s because they observe
clock R running fast relative to clocks G and B. But why does the greater time on R make sense to the G and B
observers who observe clock R running slow relative to their clock?
Why the observations aboard G agree with relativity theory
The observers aboard space station G reach the following conclusions based on the times and distances they observe in
frame G. They observe space station R move 3.75 ls away from G as the time in G advances from 0 s to
6.25 s. Thus they observe that R has a velocity of (3.75 ls / 6.25 s) = .6 c. They then
conclude from relativity theory that clock R should be advancing at only
(1−.6) = .8 times the rate of clock G,
so that the time on R should be (.8 · 6.25) = 5 s, which is what they observe.
They also observe that as space station B moved from station G to station R it traveled 7.5 ls through
frame G in (12.5 s − 4 s) = 8.5 s and therefore had a velocity relative to G of
(7.5 ls / 8.5 s) = .882352941 c, which would cause it to run very slow relative to clock G.
According to relativity theory and the observers in frame G, it should advance at only
(1−.882352941) = .470588235 times as fast as the frame G
clocks and therefore advance only (.470588235 · 8.5 s) = 4 s, which is exactly what
clock B does for reasons much different from what the G observers think. They think the relativity theory explanation
for the slowing of clocks R and B is correct because it agrees with their observations.
Why the observations aboard B agree with relativity theory
Aboard space station B the observers see G and B together when clock G reads 4 s and clock B
is set to 4 s. They subsequently observe that space station R moves 3.75 ls to B in
(8 s − 1.75 s) = 6.25 s with a velocity relative to B of
(3.75 ls / 6.25 s) = .6 c and that clock R advanced only 5 s while time in
frame B advanced 6.25 s. Therefore, aboard B the observed ratio of the rate of time in R to the rate of time
in B is (5 s / 6.25 s) = .8, which is the ratio predicted by observers in B using relativity
theory, which predicts the ratio should be (1−.6) = .8.
Aboard B it is also observed that clock G moves 7.5 ls relative to B and advances only 4 s while clocks
in frame B advance 8.5 s (from 4 s to 12.5 s). Therefore, aboard B it is observed that G is moving
relative to B with a velocity of (7.5 ls / 8.5 s) = .882352941 c and that clock G is
advancing at only (4 s / 8.5 s) or .470588235 times the rate of clocks in frame B. This is the ratio
of clock G's rate to clock B's rate expected by the observers aboard B using relativity theory, which predicts
the ratio should be (1−.882352941) = .470588235.
Conclusions from this clocks paradox example
Therefore, due to the observers' assumption of constant light speed, c, and the resulting asynchronizations of clocks
in reference frames G and B, and the foreshortening of the distance scales in frames G and B, and the slowing of clocks due
to their speed through the quantum medium, the observations of all the observers make sense to them. The observed slowing of
the other clocks relative to their clock appears to be caused by the velocities of the other clocks relative to their clock.
The people aboard space station R observe the real phenomena occurring in the example because R is at rest in the qm.
They observe the real slowing of clocks G and B due to the .6 ca velocities of G and B through the qm.
Aboard G and B the people observe a virtual slowing of clock R and a combination of real slowing and virtual slowing
of B and G due to the motions of B and G through the qm. The example shows that the observations aboard G and/or B
must be false observations because clock G and/or B must have been advancing slower than clock R because
clock R was reading 10 s when B was reading 8 s. Therefore, relativity theory must be flawed in some way
because in this R‐G‐B example it causes observations that must be wrong.
The qm view shows what is wrong. It shows that the physical changes in systems moving through the qm, and the
constant light speed c assumption, cause the observation of false, virtual phenomena that are in agreement with
relativity theory. The virtual phenomena are consistent with relativity theory's conclusion that universal, absolute times
and distances do not exist (e.g. there is no absolute distance between R and B when G is at R, and no absolute time
for B to go from G to R because the observed distance and time depends on the motion of an observer's reference frame).
The qm view also shows that absolute times and absolute distances exist in the universe and that the spacetime system
of relativity theory has been unnecessary and misleading.
If the observers on space stations R, G, and B understood the qm view and were aware of vRa or vGa or
vBa, they could then convert the virtual times and distances specified by their physical standards of time and distance
(i.e. their atomic clocks and radar ranging instruments) into absolute times and distances on which they would all agree.
All the atomic clocks in a reference frame could be absolutely synchronized and calibrated to read absolute times, and the
radar ranging instruments could be calibrated to read absolute distances. This would eliminate the great confusion inherent
in working with virtual times and distances, and it would result in the observation of true or real phenomena rather than
virtual phenomena. (On Earth our absolute velocity is constantly changing but it is probably very low. Therefore, if we
consider Earth at rest in the qm, the resulting observed, virtual phenomena are probably very close to the real phenomena.)
As you can see, the qm view explains how observers aboard G and B can observe clock R running slower than their
clock and also observe a 10 s time on clock R that is greater than the 8 s sum of the elapsed times on clocks
G and B. Their observations are the result of a complex combination of factors caused by the quantum medium. These factors
combine to yield exactly the observed virtual phenomena that are predicted by relativity theory and consistent with
experimental evidence. The fact that the combination of causes always yields the observed virtual phenomena regardless of the
observed velocities of R, G, and B relative to one another and regardless of their absolute velocities through the quantum
medium is evidence that the causes specified by the qm view are the actual causes in nature. And the twins/clock paradox
is only one of a variety of perplexing phenomena that are explained by the qm view and are therefore evidence of the
quantum medium.
|
|
Elsewhere on the qm view website at least one clock-paradox example is provided in which all three clocks are moving
through the quantum medium. The Introduction, Part II video contains such an example. These and other more
complex examples make it clear that the qm view exactly explains the physical causes of the slowing of a clock making a
round trip, and that the qm view does not result in the twins/clock paradox that is inherent in relativity theory due to
relativity's relative-motion explanation for clock slowing.
The qm view explains physical causes for the observed change in a clock's rate when the relative velocity between
clock and observer is changed. It distinguishes between two different kinds of observed clock rate change: rate change
due to changing the clock's velocity, and rate change due to changing the observer's velocity. In the first case the clock
rate change is real and in the second case the clock rate change is virtual, but relativity theory cannot distinguish between
these two cases and it obscures the completely different physical causes of these two kinds of observed clock rate change.
Hopefully the above explanation, the Equations page, the Facts page, the qm view videos, and other information will
interest people in determining for themselves whether the qm view or relativity theory is the more plausible
representation of nature. Surely many will not be interested in such an analysis because they are certain that relativity
theory is correct. Davies appears to be one whose views on this matter cannot be changed, as you can see by reading
chapter 2 of his book. And most physicists may share Davies' certainty that relativity theory is sound due to its
agreement with most experimental results. It will be interesting to see if the prevailing confidence in relativity theory
continues or can be changed as people find that the qm view is much more plausible because it reveals logical physical
causes for the observed phenomena it predicts.
To return to qm view, close tab or browser 
|
|
