Few people would deny that relativity theory has been very useful during the past century.  However, relativity theory has characteristics that caused many to wonder if something in the theory was wrong.  For example, the theory is based on a "light postulate" that assumes a logically impossible phenomenon: photons that have the same isotropic speed, c, through each of many inertial reference frames that are all moving relative to one another.  This assumption, on which so much physics theory depends, cannot be explained by orthodox physics theory.  Nevertheless, light speed, c, became a law of physics around 1900.

This strange measured speed of light, c, is explained by a quantum medium, qm, through which photons and all other energy quanta are propagated at a constant absolute speed, ca, when not slowed by mass/energy in this medium.  (During the 20th century, students of science learned reasons for believing that light is not propagated through a medium.  This web page, and the entire qm view website, show that this belief has been misleading.)  The measured speed of light, c, is a virtual speed that is the same in all inertial systems due to a combination of causes, including different standards of time and distance in systems with different velocities through the qm. 

The qm view also explains why some other aspects of relativity theory discussed below are similarly misleading.  For example, relativity theory indicates that relative motion between an observer and an observed system causes an observed foreshortening of the system.  The qm view predicts exactly the same observed, virtual phenomena that special relativity theory predicts, but it also explains the real, absolute, physical phenomena causing the virtual phenomena.  The explanation is complex, like many scientific explanations for phenomena that appeared to have simple causes.  A complete explanation is available at the qmview.net website.

The light postulate of relativity theory is responsible for the various paradoxes inherent in the theory.  It is responsible for what is often known as the "barn and pole paradox."  We will describe a similar "tube and rod" paradox that helps understand the causes, which are traceable back to misleading experimental evidence of constant light speed, c.

Tube and rod paradox
Figure 1 shows a large experimental apparatus floating in space.  It consists of a transparent, light-blue, square tube and an opaque, darker-blue, square rod that is initially floating motionless inside the tube.  (During the experiment, the rod will be moving rapidly through the tube, from right to left.)  The tube is 300 meters (m) long and the rod is 301 m long, including the 45° beveled ends.  To help explain the experiment, we can imagine an x axis on which the long axes of the tube and rod are located, and a y axis in the plane of the x=0 ends of the tube and rod, as shown.  Red and blue laser light sources, s, emit beams of light across the ends of the tube if the rod is not blocking the light path.  Photons that are not blocked are reflected by mirrors, m, attached to the tube, and the photons travel to detectors located midway between the ends of their respective tube or rod.
The detectors include light sensors, an atomic clock, a computer, and memory.  They detect incoming photons from both directions along the tube and rod, and knowing the length of the light path and light speed, c, they determine and record exactly when the ends of the rod enter and exit the tube.  The tube's detector light is green only when the detector has learned that the x=301 end of the rod has entered the tube and has not learned that the x=0 end of the rod has exited the tube (i.e. when the entire rod is inside the tube, making the rod shorter than the tube).  Consequently, if the rod moves slowly through the tube, the tube's detector light will never be green because the detector will learn that the x=0 end of the rod exited the tube before learning that the x=301 end of the rod entered the tube.  Observers aboard the tube believe that light travels between the tube's ends and the tube's detector with speed, c, and therefore believe that their detector light will be green for the same amount of time that the rod's ends are both between the tube's ends.

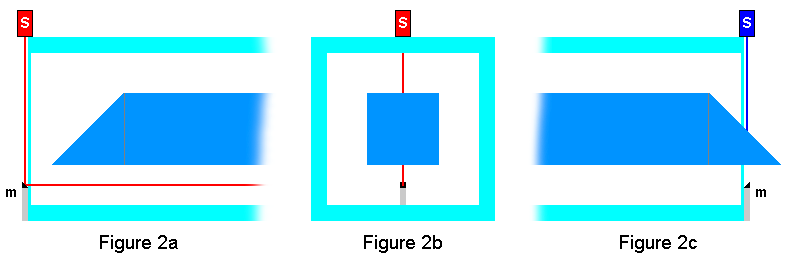
Figure 2a is an enlargement of the x=0 ends of the tube and rod showing that when the end of the rod is inside the tube, the light from source, s, is reflected by mirror, m, toward the detectors at the centers of the tube and rod.  Figure 2b is a cross section view of the apparatus looking from the detectors toward the red light source.  Figure 2c shows that when the end of the rod is outside the tube, the laser light is blocked from reaching the detectors.  (The thin ends of the rod act like shutters at the mirrors.)  The rod's detector light is green only when the detector has learned that the x=0 end of the rod exited the tube and has not learned that the x=301 end of the rod entered the tube (i.e. when the rod is protruding from both ends of the tube, making the tube shorter than the rod).  If the rod moves slowly through the tube, the rod's detector light will be green for only 1 m of the rod's 601 m journey through the tube.  Observers aboard the rod believe that light travels between the rod's ends and the rod's detector with speed, c, and therefore believe that their detector light will be green for the same amount of time that the tube's ends are both between the rod's ends.
This experimental apparatus permits the assumptions and conclusions of relativity theory and the qm view to be investigated by having the rod move far in the +x direction, and then accelerate in the −x direction and coast through the tube with high relative velocity.  The tube's detector will receive enough information via the starting and stopping of the light from the mirrors to determine the relative velocity and the length of the rod (and vice versa).

If the relative velocity between the tube and rod is observed to be six tenths the speed of light (.6 c), for example, then relativity theory and the qm view both specify that "observers(c)" (who assume that the law of constant light speed, c, and relativity theory are correct) will make observations that depend on whether the observers(c) are with the tube or with the rod.

Observers(c) with the tube will observe that the rod is shorter than the tube.  The rod's trip through the tube is so quick (3.0044.. microseconds, µs, from start to finish) that the observers must rely on instrumentation to "observe" what occurs.  The tube's detector and indicator light will show that the rod was totally inside the tube for .3288.. µs (where ".." means "endless repetition of the last two digits").  All observations by observers(c) aboard the tube (via clocks, radar, cameras, etc.) will show that the situation pictured in Fig. 3 occurred when the two detectors were momentarily next to one another.

If the tube happens to be at rest in the qm, then Fig. 3 also shows the real, absolute situation in the qm because the speeds of light relative to the tube are 3E8 m/s in all directions, as the observers(c) and instrumentation aboard the tube assume.  To simplify the following explanation, we will assume that the tube is at rest in the qm, and therefore has an absolute velocity, va=0 ca.  This results in atomic clocks aboard the tube keeping absolute time in absolute seconds, sa, and absolute microseconds, µsa.  It also results in the observers(c) with the tube unknowingly observing the real, absolute phenomena that occur during the experiment.  It results in their observing the real, absolute velocity of the rod (va=.6 ca).  This absolute velocity of the rod causes the real foreshortening of the rod shown in Fig. 3.  The physical causes of this foreshortening are explained elsewhere on this website.  The rod is foreshortened to .8 times its length when at rest in the qm.  This .8 ratio is equal to sqrt(1−va).  Therefore, the rod is (.8 * 301 m) or 240.8 ma (absolute meters) long, although observers(c) with the rod will still measure a 301 m virtual length.

Figure 3 shows the situation when the detectors at the middle of the tube and rod are aligned.  This situation occurs at 1.5022.. µsa after absolute time ta=0 sa (when the x=0 end of the rod was aligned with the x=300 end of the tube).  During part of this time, the rod moved 240.8 ma until its 301 m end was at the 300 m end of the tube.  Then it moved another .5 * (300 − 240.8) ma or 29.6 ma inside the tube until the detectors were aligned.  During the rod's 29.6 ma travel inside the tube with .6 ca relative velocity, the blue laser light from the mirror traveled (29.6/.6) or 49.33.. ma toward the detectors, as shown.  (We will ignore the small light-travel distances prior to the mirrors because they are the same at each end of the tube.)  In Fig. 3, the tube's detector light is off because the photons from the blue source have not yet reached the detector.  It should be noted that the blue light traveled a distance along the rod that is only 40% of the distance it traveled along the tube and through the qm.  This is due to the rod's .6 ca velocity relative to the tube and qm.  This will significantly affect observations on the rod.  It will cause the detector and observers with the rod to observe a foreshortened tube (as the following will show).

At ta=1.8377.. µsa, the tube's detector light comes on when the blue laser light from the x=300 m location arrives at the tube's detector.  Figure 4 shows the situation at ta=1.9175 µsa when the light from the red laser stops arriving at the rod detector.  This causes the rod detector's indicator light to go on because the detector has learned that the rod is outside the x=0 end of the tube, but has not learned, via the blue laser light, that the x=301 end of the rod has entered the x=300 end of the tube.
Observers(c) with the rod observe virtual phenomena, not the real phenomena represented by figures 3 and 4.  They observe the contracted tube shown in Fig. 5.  Not until .423611.. µsa after Fig. 4 (which shows the red light telling the rod's detector that the x=0 end of the rod has exited the tube) does the blue laser light arrive at the rod detector and cause its light to go off.  The reason for the long delay in receiving the blue laser signal is that the signal velocity relative to the rod is only .4 ca due to the rod's .6 ca absolute velocity through the qm.  Conversely, the rod's detector received early notice of the rod's x=0 end exiting the tube due to the 1.6 ca velocity of the red laser light relative to the rod.  The .423611.. µsa difference between the arrival times of the two signals at the rod detector is the time on atomic clocks at rest in the qm.  This time duration is equal to (.8 * .423611.. µsa) or .3388.. virtual µs on the rod detector's clock, which is advancing at only .8 times the rate of the tube detector's clock due to the rod's −.6 ca absolute velocity.

Therefore, observations on the rod show that the x=0 end of the rod emerged from the x=0 end of the tube .3388.. µs before the x=301 end of the rod entered the tube.  The observers and instruments on the rod therefore conclude that the tube is (.3388.. µs * .6 c) = (.3388.. µs * .6 * 300 m/µs) = 61 m shorter than the rod, which means to them that the tube is (301−61) or 240 m long.  This is .8 times the length of the tube when it was at rest relative to the rod, and this is what they expect because relativity theory tells them that the tube should contract by 20% due to its .6 c relative motion.  The qm view shows that this is a totally virtual contraction and that the tube's length did not change during the experiment.
The tube and rod paradox, and the other paradoxes of relativity theory, are evidence that the law of constant light speed, c, and relativity theory are not creating a realistic picture of nature.  The qm view shows that the primary cause of the conflicting observations of the observers(c) is the different speeds of light in the reference frames of the tube and rod.  The reader should be aware of the remarkable fact that observers(c), whether with the tube or the rod, will always observe the same foreshortening of the rod or tube regardless of the absolute velocity of the tube through the qm.  If readers learn about the causes of the tube and rod paradox, it will become clear that the primary cause is the light speed, c, illusion.

The light speed, c, assumption is responsible for the disagreement between observers(c) who are moving relative to one another.  The qm view shows that this disagreement is unnecessary if the observers understand what is causing their disagreement.  The primary cause is the different speeds at which energy quanta are moving through their reference frames.  It is not relative motion, as the above example shows.  Had the tube's absolute velocity been .6 ca in the +x direction, the −.6 c virtual velocity of the rod relative to the tube would have resulted in the rod being at rest in the qm as it was traveling through the tube.  The rod would have been 301 ma long and the tube would have been 240 ma long (as in Fig. 5), but the observations of the observers(c) would have been exactly the same as when the rod was 240.8 ma and the tube was 300 ma.  The observers(c) are unaware that their virtual observations can be caused by an endless number of combinations of tube and rod absolute velocities.  They are unaware that their virtual observations are "shadows" of the absolute phenomena causing them.  They know only that their relative motion is causing observations specified by relativity theory, and that the theory must be correct because it agrees with their observations.

The light speed, c, assumption has profound theoretical and philosophical consequences.  It means that universal standards of time, distance, and mass, on which observers throughout the universe can agree, are impossible.  It means that all observers who are moving relative to one another have their own standards of time, distance, and mass and therefore have different pictures of reality having different orders in which events occur and different sets of masses for all the bodies in the universe.  The law of light speed, c, resulted in the elaborate and no-longer-necessary system of spacetime, which the relativity paradoxes and other evidence indicate is not in accord with nature (in spite of being useful).  The qm view, and the related evidence, show that the classical view of nature, having space and time with universal units of distance and time, is far more logical and plausible.

The above discussion is an attempt to show that the light speed, c, assumption of relativity theory is the underlying cause of the relativity paradoxes, and we will now consider another experiment that shows the fallacy of this assumption.


Experimental test of constant light speed, c
The qm view website shows that the view it specifies is not only in mathematical agreement with a wide variety of important phenomena, but also explains logical physical causes for the phenomena, which have been a mystery.  The extensive evidence supporting this view is also evidence that the speed of light, c, is a virtual light speed caused by different physical standards of time and distance in different reference frames.  In spite of this extensive evidence, many may want additional evidence that photons are propagated through a medium and therefore do not have a constant speed relative to bodies moving through this medium.  Possibly, an experiment similar to the following could make this more obvious.

Experiment description
This imaginary experiment involves two square, rigid tubes that are 100 m long.  The tubes are designated R and B and are initially located next to one another in a zero-gravity environment in space.  Figure 6 shows the x axis of their coordinate system midway between adjacent edges of these gray tubes.  Red and blue light sources are located on the coplanar sides of the tubes that are visible in all the figures below.  The tubes have distance marks every meter.
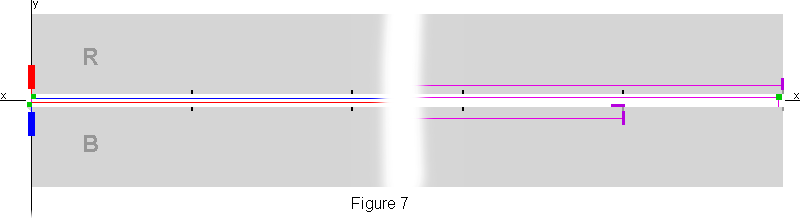
During the experiment, light from the sources will be traveling to light detectors (e.g. photodiodes) mounted on the same sides of the tubes.  Figure 7 shows the arrangement of the optics at the source and detector ends of the tubes.  It also shows the light paths of the photons from the sources to the detectors.  The sources are colored red and blue to represent the two different source frequencies so that the two sources can be distinguished by the three detectors, which are represented by the purple rectangles. 

The light from the red source on tube R travels in the plane of the end of tube R toward tube B.  Similarly, the light from the blue source travels in the plane of the end of tube B toward R.  The green squares represent mirror assemblies that redirect the red or the blue light beams 90 degrees toward the detectors.  The light paths from the sources to the detectors are essentially coplanar (except from source to mirror, where the paths have slightly different distances from the x axis, permitting each mirror to reflect the light from the other tube without blocking the light from its tube).

The experiment involves sending tube R past tube B with an observed relative velocity of −.0101.. c (or 3030303.03.. m/s if we say c=3E8 m/s).  This velocity permits light to be sent 99 m along the x axis in 330 ns while R moves −1 m relative to B.  To prepare for the experiment, tube R is moved far away in the +x direction and then accelerated in the −x direction until it attains the .0101.. c relative velocity at which it coasts past tube B. 

What the qm view predicts
When the source end of tube R arrives at the y axis, the first photons of a pulse of red light are reflected by the mirror on B, and the first photons of a pulse of blue light are reflected from the adjacent mirror on R.  These initial photons begin traveling along the x axis together, and if the tubes were not moving relative to one another the initial photons would reach the x=100 ends of the tubes simultaneously. In the qm view, when R is moving with the −.0101.. c velocity relative to B, the first photons from the R and B mirrors will also leave the mirrors together and travel together with equal speed through the qm and equal speed along the x axis of the x-y coordinate system.

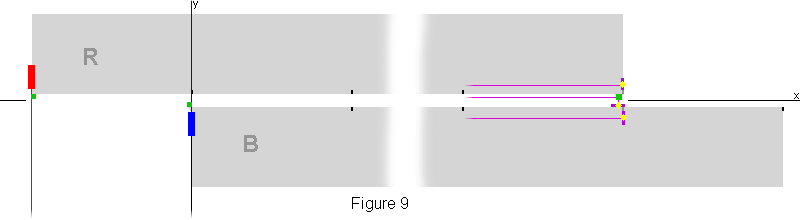
As the light pulses move along the x axis, their patterns broaden and the photons arriving at the detectors on R and B are a mixture of photons from the red source and photons from the blue source. The purple lines going to the detectors in figures 8 and 9 represent this mixture.

A light (yellow) on each detector flashes very briefly during the experiment to show when photons from the sources are arriving at each detector.  If the light pulses are 1 m long, the duration of the flashes will be about 3 ns, and a human could not see that the flashes occur simultaneously.  Therefore, the detector lights shown in Fig. 9 are symbolic, and we must rely on the instrumentation at the detectors to record when the first photons from each source arrived at each of the three detectors.  In the qm view, the detectors will show that the first photons from the two sources arrive at the three detectors essentially simultaneously, and that all the photons had essentially the same speed along the six light paths in the x-y coordinate system. 

The arrival of the first photons at the two detectors that are transverse to the x axis is essentially simultaneous because the light paths are the same length in the x-y coordinate system.  The light path via the mirror near the x=100 end of R is also the same length, so the first photons from sources R and B should also arrive simultaneously at both detectors on B and at the detector on R.  Any differences between the arrival times at the three detectors should be easily detectable via communication between the adjacent detectors on B.  In the qm view, the detectors will show that the first photons arrived simultaneously at all three detectors, which means that they traveled 100 m along R while they traveled 99 m along B, and that they therefore traveled faster along R, which shows that the speed of light in all inertial frames is not constant.

The qm view shows why the length of tube R will be about 5 cm longer or shorter than tube B when the tubes pass with .0101.. c relative velocity.  This length change will have no significant effect on the outcome of the experiment, and we mention it to show that it has been considered.


What the law of light speed, c, predicts
According to orthodox theory based on light speed, c, the first photons of the red and blue light pulses will not travel together because they will leave the mirrors with the same velocity, c, relative to the mirrors, and because mirror R has a .0101.. c velocity in the −x direction relative to mirror B.  Therefore, the blue photons from mirror R will move about 3E6 m/s slower toward the detectors than the red photons from mirror B.  This will cause the first blue photons to arrive at the detectors about 3.3 ns after the red photons arrive.  The detectors can detect differences in arrival times and therefore show whether or not the photons are traveling together from sources to detectors.

Other considerations
Those who doubt that the photons will travel together might consider the evidence from binary stars where the photons emitted from the stars must be traveling at the same speed to Earth in spite of the fact that the photons' sources have significantly different velocities toward or away from Earth (just as the mirrors on tubes R and B have different velocities relative to the detectors). If the photons from the binary stars did not travel together through the cosmos, the photons would not arrive on Earth in the understandable patterns that are observed.  Photons that were emitted nearly simultaneously at the binaries would be arriving on Earth days or years apart.

Another indication that the photons leaving the mirrors simultaneously travel together along the tubes is that the qm view and orthodox theory both predict that the blue photons will be redshifted due to the velocity of tube R relative to tube B.  This redshift can be determined by comparing the frequencies of the blue photons detected during the experiment with the frequency detected when tube R was at rest in the x-y system as shown in Fig. 7.  In the qm view, the redshift of the blue photons is explained exactly by tube R's velocity in the −x direction relative to tube B.  This velocity results in the blue photons leaving the tube R mirror with a relative velocity that is greater than the relative velocity at which they arrive at the transverse detector on tube B, and this results in lower-frequency photons absorbed at this detector.  The law of light speed, c, makes this redshift impossible (unless some other physical cause for the redshift can be identified).

Readers should keep in mind that observers(c) aboard tubes R and B who measure the speed of light along their tubes will always measure the same virtual speed, c, in spite of the observed .0101.. c relative velocity between the tubes.  Physical causes for this observed constant speed of light are explained by the qm view, as most readers of this page realize.  It should also be kept in mind that the law of light speed, c, is inconsistent with considerable, verifiable evidence, as well as logic.  When it becomes clear how constant light speed, c, can be a misleading illusion, a wide variety of perplexing phenomena become understandable and logical.  Throughout history, science has gradually raised the levels of human awareness, and the qm view appears to be an opportunity to improve this awareness by correcting the misconceptions caused by the illusion of light speed, c.

Light speed, c, illusion © 1994-2014 by P. F. Allport is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.
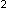