The following assumes that the reader understands why the absolute velocity, va, of a system of mass/energy through the quantum medium, qm, causes a foreshortening of the system along lines parallel to va and causes a slowing of all clocks and other processes in the system, and that the foreshortening and slowing are proportional to the change in physical change ratio, which is Δrv = 1− sqrt(1− va).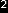

Imagine a huge, simple, light-speed-measuring apparatus (shown in cyan color in the figure below). The apparatus is at rest in the qm and therefore has absolute velocity va=0 ca, as shown. This "at-rest" case is special because it is the only case in which observers on the apparatus will observe the real phenomena occurring in their reference frame. Only in this case, is the virtual, constant speed of light, c, (determined by the apparatus and observers) the same as the real, absolute speed of light through their reference frame.

In this at-rest case in the figure, the apparatus is one absolute light-second long, which is the distance that light travels through the qm in 1 absolute second. This distance is designated 1 LS, as opposed to a virtual light-second designated 1 . An absolute second is 1 second according to an atomic clock at rest in the qm and it is designated 1 sa, as opposed to a virtual second designated 1 s. This terminology will become clearer below.



The apparatus will be used by the observers to determine the speed of light from a star (at left end of figure).

The observers know that light always travels through their reference frame with speed c, which is 3E8 m/s or 1 /s. We will designate observers who know this "observers(c)."

The apparatus has a distance scale with 0 at the mark at one end and 1 at the mark at the other end, as shown. At each end of the scale an atomic clock and other instrumentation (e.g.  light emitter and detector) is used to determine the departure and arrival times of light signals.

Preparing the measuring apparatus
Observers(c) can check the length of the distance scale by sending a light signal from 0 to a mirror at 1 and measuring the elapsed time on the 0 clock for the signal to arrive back from 1 . We know from the above that this round-trip time will always be 2 s on the clock.  We also know that the observers could, in theory, check the 1 length of the distance scale by using 299,792.458 1-kilometer-long measuring rods placed end to end, because a meter is defined as the distance traveled by light in vacuo in (1 / 299792458) second.

Synchronizing the 0 clock and 1 clock is easily done by sending a signal containing the 0 clock time, t s, from 0 to 1 . When this signal is received, the 1 clock is set to (t+1) s to allow for the 1 s travel time for the signal.

The distance scale is aligned with a line from the apparatus to the star. Therefore, photons from the star that pass the 0 mark also pass the 1 mark.

The apparatus has a shutter at 0 , and when the shutter is closed the starlight is stopped from continuing to the 1 location.

Checking the speed of light when va=0
To check the speed of light arriving from the star, the shutter is opened briefly to permit light to travel to a mirror at 1 . As the shutter opens and the first starlight begins traveling to 1 , the departure time, t s, on clock 0 is recorded. And when the reflected first light returns from 1 , the arrival time, (t+2) s on clock 0 is recorded. The observers(c) also expect and confirm that the arrival and departure time of the reflected first light at the mirror is (t+1) s on the 1 clock. Their observations show that the speed of light along the x axis is 1 /s.



Why observed light speed is c when va≠0
Now we conduct the same imaginary experiment with the same apparatus and same observers, except the apparatus is moving in the +x direction with absolute velocity va=.6 ca through the qm.

Due to va=.6 ca, the speed of light relative to the apparatus, cr, is not constant. It depends on the direction of travel of the light through the reference frame of the apparatus. Along the x axis of the apparatus in the +x direction, cr=.4 ca (white vector minus cyan vector). And in the −x direction it is 1.6 ca (white vector plus cyan vector). Along the y axis, or in any other direction transverse to the x axis, cr=.8 ca for reasons explained elsewhere. This anisotropy of cr (i.e. having different relative velocities of cr in different directions) due to va=.6 ca occurs at all levels of mass/energy in the apparatus. It occurs at the lowest level where the oscillations of the qm comprising energy quanta are moving with cr=.4 ca in the +x direction of the apparatus reference frame and cr=1.6 ca in the −x direction. The anisotropy causes physical changes within the apparatus. The physical change ratio, rv, specifies the rate of round-trip energy exchange at all levels of mass/energy in the apparatus, as explained elsewhere on this website. When va=.6 ca, rv=.8  as specified by the equation in the following figure.


Physical changes in time and distance
This results in a slowing of the clocks and all other processes in the apparatus reference frame to .8 times their at-rest rate. This is explained in the qm view introduction video and elsewhere. A clock at rest in the qm keeps time in "absolute second" units, sa. Clocks moving through the qm keep time in "virtual second" units, s, that depend on va and rv. Therefore, 1 s is not a fixed absolute time and can be from 1 sa up to large absolute time durations. One s on an atomic clock with va=.99 ca is 7 sa, and when va=.999999 ca, 1 s on the clock is 707 sa (via the rv equation and knowing that a clock's s/sa rate is equal to rv).

The change in rv also specifies the foreshortening of the apparatus in the x direction to .8 times its at-rest length. Therefore, the distance between 0 and 1 is now only .8 LS, as shown.

Asynchronization of clocks
Due to va=.6 ca and the resulting rv=.8, and the constant-light-speed-c assumption of observers(c), clock 0 and clock 1 become asynchronized (i.e. not synchronized) when they are "virtually synchronized" by observers(c). The reasons are as follows. A light signal that is sent from 0 when clock 0 reads t s, takes 2 sa to reach clock 1 because the distance between 0 and 1 is .8 LS and because the speed of light from 0 to 1 is cr=.4 ca, and (.8 LS / .4 ca) = 2 sa. Therefore, when the 1 observers(c) receive the t s signal from 0 and set their 1 clock to read (t+1) s (as they did when va=0), the 0 clock has advanced (.8 · 2 sa) or 1.6 s and reads (t+1.6) s. Consequently, after the virtual synchronization, clock 1 is .6 s behind the time on clock 0 , as shown. The same asynchronization will occur if the observers(c) at 0 synchronize their clock with clock 1 via a time-encoded signal from clock 1 .

Conclusions
With their clocks apparently synchronized, the observers(c) are ready to measure the speed of the starlight through their reference frame. When the shutter at 0 is opened at time t on clock 0 , the starlight begins traveling toward 1 , and 2 sa later it arrives at the mirror at 1 when clock 1 reads [ (t−.6) + (2 sa · .8) ] or (t+1) s, as expected. The light is reflected back toward location 0 , and takes only .5 sa to travel the .8 LS distance because cr=1.6 ca. Therefore, the round-trip travel time for the light is 2.5 sa, during which time the 0 clock advances 2 s, as the observers(c) expect. Their observations confirm that the speed of light in both directions along the x axis of their reference frame is 1 /s.

The observers(c) will always determine that the speed of light from the star is 1 /s regardless of the absolute velocity of the apparatus. The Constant Light Speed, c  video explains this in detail. This is part of the strong evidence that constant light speed, c, is very likely an illusion. The above information indicates that the belief in light speed, c, is like a self-fulfilling prophecy because it creates assumptions that lead to physical evidence of constant light speed, c.
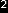